摘要:高斯分布分析在自然科学与行为科学里有着广泛应用。高斯分布是一个在数学、物理及工程等领域都非常重要的概率分布,由于这个分布函数具有很多非常漂亮的性质,使得其在诸多涉及统计科学离散科学等领域的许多方面的分析上都有着重大的影响力。我们可以用高斯分布分析来对计量误差、学生平均身高的高矮概率这些生活里的事件进行分析,也可以用于科学领域对动态光散射法(DLS)的粒度表征结果进行分析。
关键字:高斯分布分析、计量误差、动态光散射、Nicomp 380、平均直径与标准偏差
前言
高斯分布是自然科学与行为科学里定量现象的一个方便模型。各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从正态分布。正态分布分析出现在许多区域的统计,例如:光子计数、计量误差、生物标本的物理特征、测试和身高分布等。
高斯分布被誉为"上帝的分布", 其强悍的建模能力和优美的数学性质使得高斯分布分析在现实中得到广泛的应用。由中心极限定理可以知道, 大量独立同分布的随机变量的均值在做适当标准化之后会依分布收敛于高斯分布, 这使得高斯分布分析具有广泛的普适性。
高斯分布分析
高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,由于这个分布函数具有很多非常漂亮的性质,使得其在诸多涉及统计科学离散科学等领域的许多方面的分析上都有着重大的影响力。比如图像处理中最常用的就是滤波器类型为Gaussian滤波器。
若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布,记为:
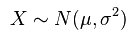
其概率密度函数为:
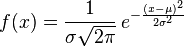
则其为高斯分布。高斯分布的数学期望值或期望值μ等于位置参数,决定了分布的位置;其方差σ2的开平方或标准差σ等于尺度参数,决定了分布的幅度。
正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数μ=0,尺度参数σ=1的正态分布(见右图中绿色曲线)。
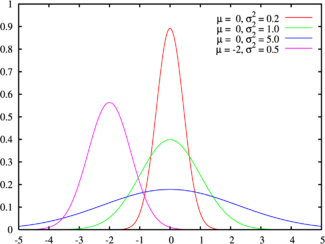
图1 高斯分布图片
高斯分布分析计量误差
有一个饮料公司装瓶流程严谨,每罐饮料装填量符合平均600毫升,标准差3毫升的高斯分布分配法则。随机选取一罐,求解(1)容量超过605毫升的概率;(2)容量小于590毫升的概率。
容量超过605毫升的概率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 1 - 0.9525 = 0.0475
容量小于590毫升的概率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004
高斯分布分析学生身高的高矮概率
某校入学新生的身高的平均身高与方差分别为150与14.4。随机抽取50个学生,求解他们身高的平均高度大于157.5的概率?小于135的概率?
这里没有常态分配的假设,但高斯分布的中心极限定理提供一个可行解,那就是当随机样本长度超过30,样本平均数xbar近似于一个常态变量,因此标准常态变量Z = (xbar –μ) /σ/ n1/2。
平均分数大于157.5的概率 = p(Z> (157.5 – 150) / (14.4 /501/2))= p(Z> 5/1.7) = p( Z > 2.94) = 0.0016
平均分数小于135的概率 = p(Z< (135 – 150) / (14.4 /501/2))= p(Z < 5.88) = 0.0000
高斯分布分析动态光散射法(DLS)的粒度表征结果
用PSS公司的Nicomp 380检测一个乳剂样品的平均粒径,收集的光子信号经自相关器处理,得到图2 中64个通道的自相关数据图形(相关概念可参阅GB/T 29022-2021),图形接近指数分布,但又不是完全的指数分布。
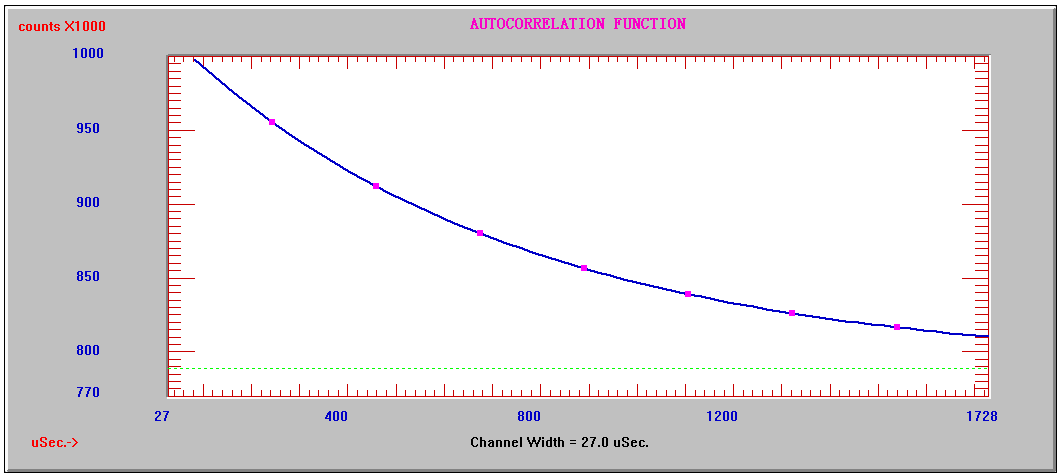
图2. 自相关函数值C(t’)作纵坐标,t’作横坐标
利用累积量的数学工具可以有效处理自相关函数的指数行为和非指数的行为,可得到自相关函数经拟合后的扩散系数分布,其类似于高斯分布形状。它是一个钟形分布,只需通过D和∆D两个参数就能完整的描述。
同时根据Stokes-Einstein关系:D = kT / 6πηR
K是玻耳兹曼常数(1.38 X 10-16 erg K-1),T是温度(0K,= 0C + 273),η是溶液的剪切粘度。
可以得到平均粒径R的类似高斯分布,同时平均直径d = 2 R,直径分布的标准偏差是2 *∆R。后一个参数是也被称为“变异系数”,等于“方差”的平方根。图3,是高斯分布分析的最终结果,平均直径d=222.61nm,标准偏差∆d/d=30%。
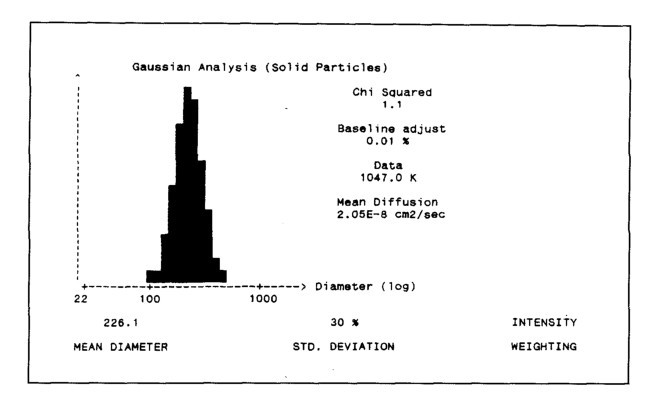
图3. Intensity-weighted高斯分布分析结果
结论
此文论述高斯分布分析的概念,以及它的三个应用。其中第三个应用,使用Nicomp 380得到高斯分布的粒度表征结果的过程,是目前市面上主流DLS原理的仪器表征结果的获取过程,其具有广适性。此文证明了高斯分布分析不仅可以应用生活中的常见场景,也可以应用于高端的科学领域,它具有广泛的应用。
参考文献
[1]. GB/T 29022-2021
[2]. 高斯分布(Gaussian distribution)/正态分布(Normal distribution)相关网址:https://blog.csdn.net/zyttae/article/details/41086773
[3]. Nicomp 380 Z3000 User Manual.2005














